The final project of my studies was the master’s thesis. It has the rather long title “Improving Efficiency in X-Ray Computed Tomography Using Compile-Time Programming and Heterogeneous Computing”.
Specifically, my task involved the open source software elsa which is developed at the computational imaging and inverse problems group at the Technical University of Munich. As I have enjoyed my involvement in Free and Open Source Software before, most notably with MoveIt, I was happy to again contribute to a larger public project.
My work was divided into two interrelated tasks both concerned with improving the efficiency in elsa:

Before diving deeper into the programming part, I will give a short primer on computed tomography.
What is computed tomography?
Due to their high energy nature, X-rays are able to penetrate objects which are opaque to the human eye. However, they not only traverse the object but also interact with its matter. This interaction is what enables X-ray imaging. Equivalent to photography, X-ray imaging captures the differences in modulation leading to results like the famous first radiograph of Röntgen’s wife hand shown in the Figure below. The bones of the hand exhibit stronger absorption compared to the soft tissue surrounding it.
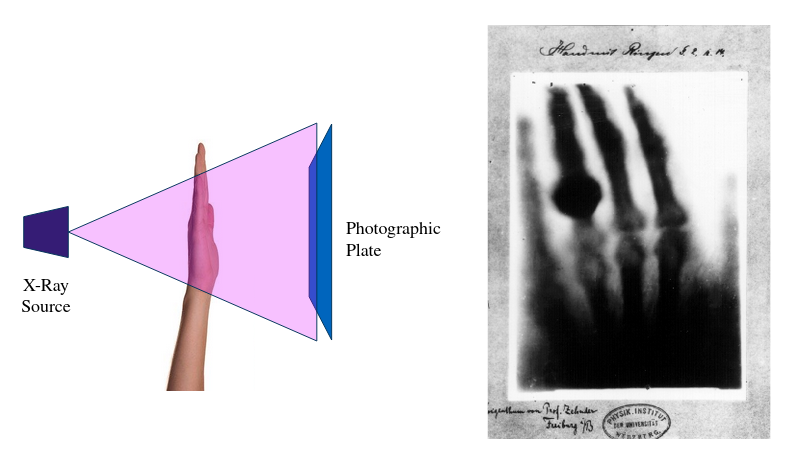
The main drawback from basic X-ray imaging is its projective nature: The measured intensity corresponds to the accumulated absorption after the ray has completely traversed the object. Therefore, all depth information is lost. This limitation is what computed tomography overcomes and achieved through taking multiple measurements of the same object at different angles. In practice, it is realized through a rotating X-ray source and detector setup as shown in the picture.
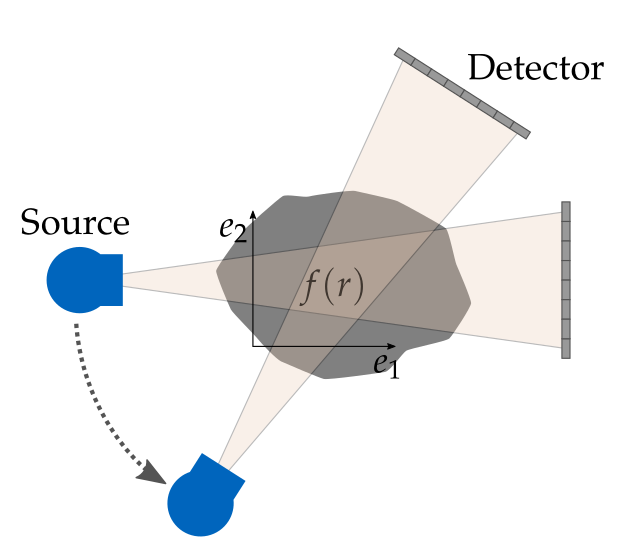
As one can imagine, combining those multiple measurements into a single 3D model is challenging. It is classified as an ill-posed inverse problem where one wants to reconstruct the causes (absorption coefficients in the object) from the effects (pixelwise intensity measurements). The inverse problem of X-ray CT falls into the category of ill-posed problems as the solution might not always be unique and small measurement errors can cause large deviations in the solution.
After discretization, the problem to solve can be expressed as simple linear equation $$ A x = y $$ where $y$ is the vector of measurements and $x$ is the linearized vector of absorption coefficients of the object. The matrix $A$ is called the system matrix and incorporates all the information about the geometry of the source as well as the detector.
At first this seems like a very easy problem: simply compute $$ x = A^{-1} y $$ and be done. However, the dimensions of $x$, $y$ and $A$ make this prohibitively expensive. A typical 3D reconstruction volume has $n = 1024^3$ elements. All of the projections taken together are in the same order of magnitude, resulting in $m = 1024^3$ measurements. This means $A$ has $m × n = 2^{60}$ entries, requiring multiple exa-bytes of memory for storing it.
Due to the problem size, computational efficiency is a core requirement for computed tomography. The programming technique of Expression Templates (ETs) is one building block for this.
Expression Templates
ETs are a compile-time programming technique to avoid intermediate results while still allowing an intuitive mathematical syntax. Consequently, all major C++ linear algebra libraries implement it. ETs are best understood following a practical example, assuming a Vector class as a wrapper around a raw array. We can define custom functions for each specific calculation as shown below:
class Vector {
...
};
Vector saxpy(float a, const Vector& X, const Vector& Y)
{
Vector result(X.size());
for(size_t i = 0; i < result.size(); ++i)
result[i] = a * X[i] + Y[i];
return result;
}
// ...
auto result = saxpy(a, X, Y);
Now, instead of having to write and call a function for each mathematical operation, we want to define operators like $+$, $-$ and so on for intuitive notation. In C++, this is easily doable with operator overloading:
Vector operator+(Vector const& lhs, Vector const& rhs) {
Vector result(lhs);
for (int i = 0; i < lhs.getSize(); ++i) {
result[i] += rhs[i];
}
return result;
}
...
Vector operator*(float lhs, Vector const& rhs);
...
float a;
Vector X, Y, A;
A = a * X + Y
However, this comes with two deficits: speed and memory. C++ implements eager evaluation which means that each operator will be evaluated on its own as soon as possible. For example in the saxpy computation, this means that two complete for loops through all elements will be executed and one intermediate result from A * x stored.
Overcoming these shortcomings is the purpose of ETs. The idea is to save the computations to be done as a type of a lightweight Expression object at compile-time. This object can then be evaluated in a single pass
and only when needed.
Let’s look at an example again:
template <Left_Operand, Right_Operand, Operation>
class Expression
{ ... };
Expression expression = a * X + Y
What is now the type of expression? It’s easier to first start with a * X which has the type
Expression<float, Vector, Mult>
and consequently the combined term has the type
Expression< Expression<...>, // a * X
Vector,
Plus>
Expression Templates for elsa
In elsa, a custom DataContainer class is used which wraps an Eigen matrix. The implementation is heavily based on the talk given by Bowie Owens at CppCon 2019. He presents ETs using modern C++17.
Internally, Eigen already implements ETs. Consequently, the task for my thesis was leveraging the Eigen internal ETs while still maintaining the elsa interface with the DataContainer class.
Results
After having implemented ETs, it is time to evaluate them. For this, incrementally longer mathematical expressions are computed with elsa. They are:
a) $x = x * y$ (a)
b) $x = x * y + y$ (b)
c) $x = x * y + y / z$ (c)
d) $x = x * y + y / z + x$ (d)
The results shown in the figure below clearly indicate the efficiency gains through using ETs compared to operator overloading. As the expressions get longer, the difference increases. The results also show that there are only slight performance penalties compared to directly using the Eigen implementation. Great!
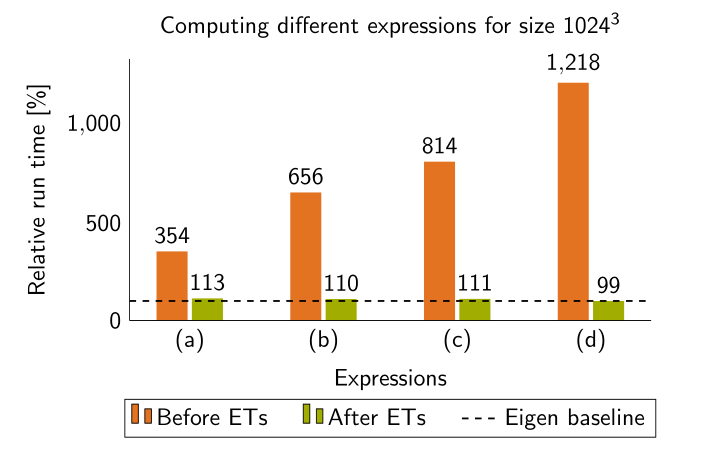
Benchmarking Expression Templates
GPU Computing for elsa
The second aspect of my master’s thesis concerned utilizing GPUs. As explained before, computed tomography deals with solving a huge linear system of equations. For this, large arrays of numbers have to be manipulated. This is the perfect task for GPUs, as they can do parallel processing in their hundreds of computational cores.
In elsa, the abstraction with the DataContainer comes in handy: depending on the user and available hardware, it can be created either in main memory (using Eigen) or on the GPU (using CUDA). However, the interface and available operations stay fixed. Therefore, the user can be as little as possible concerned with where exactly the computations happen. For him/her the DataContainer behaves the same. One challenge was that CUDA, opposed to Eigen, does not provide ETs. Therefore, my task was first coming up with CUDA enabled ETs and then integrating them into elsa as done with Eigen before.
Again, I took inspiration from the talk given by Bowie Owens. But in this case, some difficulties came up: first of all, CUDA does not fully support metaprogramming although this is a crucial feature for ETs. Second, for the ETs to be evaluated on the GPU, they need to be transfered to the GPU. Both steps required a lot of tinkering and a deep understanding of how CUDA device code works. For a more thorough discussion, you can take a look at this Gitlab issue.
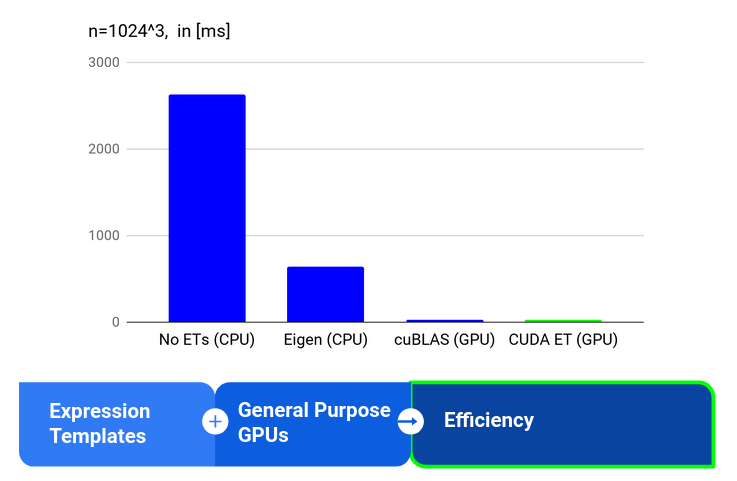
Results
The results show impressive performance for the saxpy (single precision a times x plus y) computation: on the one hand, its around 30 times faster than Eigen and on the other hand, compared to directly using a saxpy kernel, the overhead of using the DataContainer with its flexible and intuitive notation is negligible.
Conclusion
Both goals I set out to solve for my thesis where achieved: elsa now includes ETs using the Eigen internal ETs as well as CUDA with the ETs implemented by myself. It was a lot of fun working together my supervisor Tobias plus other (PhD) students on elsa. I definitely got a deeper understanding of C++, especially the metaprogramming aspects.
If you are interested in further details, you can download my full thesis.